手动性能测试
当工程师能够在开发过程中利用现有的性能测试基础设施时,这是很棒的。在前一节中,我们讨论了CI系统的一个很好的功能是可以向其提交性能评估作业的可能性。如果支持这一点,那么系统将返回测试开发人员想要提交到代码库的补丁的结果。由于各种原因,这可能并不总是可能的,比如硬件不可用、设置对于测试基础设施来说过于复杂、需要收集额外的指标。在本节中,我们提供了进行本地性能评估的基本建议。
当我们在代码中进行性能改进时,我们需要一种方法来证明我们确实取得了改进。此外,当我们提交常规代码更改时,我们希望确保性能没有退化。通常,我们通过以下方式来做到这一点:1)测量基准性能,2)测量修改后程序的性能,3)将它们进行比较。在这种情况下,我们的目标是比较同一个功能程序的两个不同版本的性能。例如,我们有一个以递归方式计算斐波那契数的程序,我们决定以迭代的方式重写它。两者在功能上是正确的,并且产生相同的结果。现在我们需要比较两个程序的性能。
强烈建议不仅获取单个测量值,而是多次运行基准测试。因此,我们有N次基准的测量结果和N次修改版本的程序的测量结果。现在我们需要一种方法来比较这两组测量结果,以确定哪个更快。这个任务本身是难以解决的,有很多方法可以被测量结果所欺骗,并且可能从中得出错误的结论。如果你问任何数据科学家,他们都会告诉你,你不应该依赖于单一的度量指标(最小值/平均值/中值等)。
考虑图@fig:CompDist中收集的两个程序版本的性能测量的分布。这个图显示了对于给定版本的程序,我们得到特定时间的概率。例如,版本A完成在大约102秒的概率约为32%。诱人的是说A比B更快。然而,这只有一定的概率P才是真的。这是因为有一些B的测量比A快。即使在所有B的测量都比每个A的测量都慢的情况下,概率P也不等于100%。这是因为我们总是可以为B生成一个额外的样本,这个样本可能比一些A的样本更快。
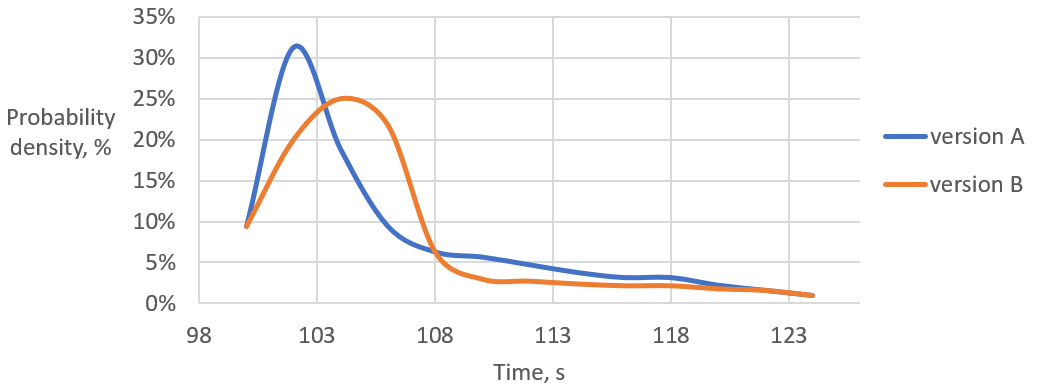
使用分布图的一个有趣优势是它允许您发现基准测试的不良行为。3如果分布是双峰的,那么基准测试很可能经历了两种不同类型的行为。双峰分布测量的常见原因是代码具有快速路径和慢速路径,比如访问缓存(缓存命中 vs 缓存未命中)和获取锁(竞争锁 vs 非竞争锁)。要“修复”这个问题,应该将不同的功能模式分离出来并单独进行基准测试。
数据科学家通常通过绘制分布图来呈现测量结果,并避免计算加速比。这样做可以消除偏见的结论,并允许读者自行解释数据。绘制分布的一种流行方式是使用箱线图(参见图@fig:BoxPlot),它允许在同一图表上比较多个分布。
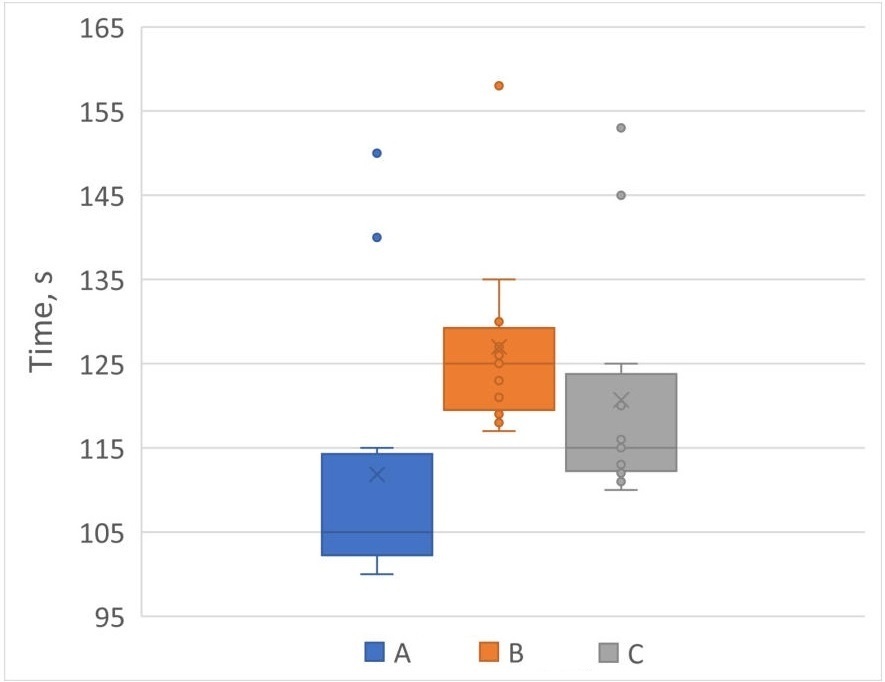
虽然可视化性能分布可能有助于发现某些异常,但开发人员不应该将它们用于计算加速比。一般来说,通过查看性能测量分布来估算加速比是困难的。此外,正如前一节讨论的那样,它在自动基准测试系统中不起作用。通常,我们希望获得一个标量值,该值代表两个程序版本的性能分布之间的加速比,例如,“版本A比版本B快X%”。
假设检验方法
假设检验方法是确定两个分布之间的统计关系的一种方法。如果根据阈值概率(显著水平),数据集之间的关系将拒绝零假设6,则将比较被认为是统计显著的。
如果分布是高斯分布(正态分布),那么使用参数假设检验(例如,学生T检验)来比较分布就足够了。尽管值得一提的是,性能数据中很少见到高斯分布。因此,在使用假设为高斯分布的公式时要谨慎。
如果要比较的分布不是高斯分布(例如,严重偏斜或多峰),那么可以使用非参数检验(例如,曼-惠特尼U检验8、克鲁斯卡尔-沃利斯单因素方差分析9等)。
假设检验方法非常适用于确定速度提升(或减慢)是否是随机的。因此,最好在自动化测试框架中使用它来验证提交是否引入了性能回归。关于性能工程统计学的一个很好的参考资料是Dror G. Feitelson的书《计算机系统性能评估的工作负载建模》12,该书有关于模态分布、偏度和其他相关主题的更多信息。
一旦通过假设检验确定了差异是统计显著的,那么速度提升可以计算为平均值或几何平均值之间的比率,但有一些注意事项。在少量样本中,均值和几何平均值可能会受到异常值的影响。除非分布的方差很小,否则不要仅考虑平均值。如果测量值的方差与均值相同数量级,那么平均值就不是一个代表性的指标。图@fig:Averages展示了程序的两个版本的示例。仅查看平均值(@fig:Averages1),很容易认为版本A比版本B快20%。然而,考虑到测量的方差(@fig:Averages2),我们会发现情况并非总是如此。如果我们取版本A的最差分数和版本B的最佳分数,我们可以说版本B比版本A快20%。对于正态分布,可以使用均值、标准差和标准误差的组合来衡量程序两个版本之间的速度提升。否则,对于偏斜或多峰样本,必须使用更适合基准测试的百分位数,例如,最小值、中位数、90th、95th、99th、最大值或这些的某种组合。
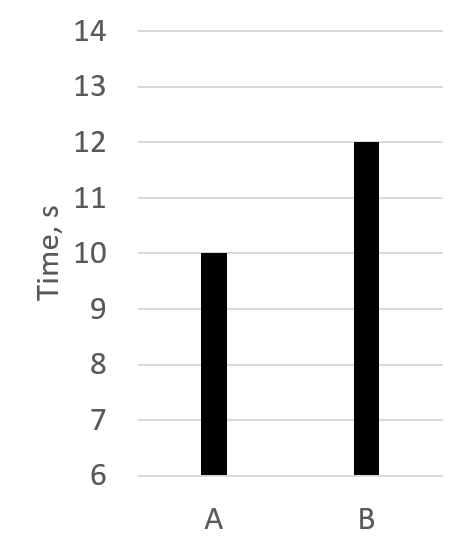
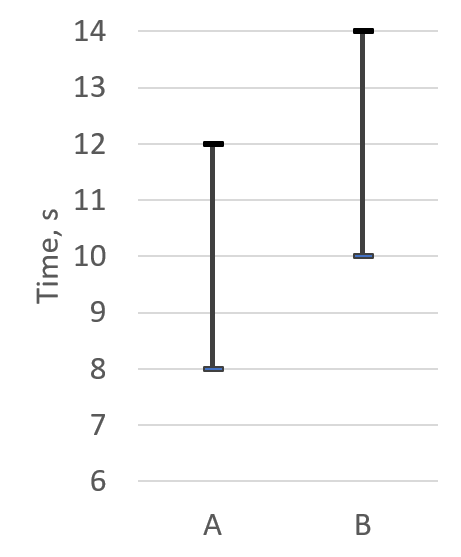
计算准确速度提升比率的一个最重要因素是收集丰富的样本集,即多次运行基准测试。这听起来可能很明显,但并不总是可行的。例如,一些SPEC CPU 2017基准测试1在现代机器上运行超过10分钟。这意味着仅生成三个样本就需要1小时:每个程序版本30分钟。想象一下,如果你的测试套件中不只有一个基准测试,而是有数百个。即使将工作分配到多台机器上,收集足够统计数据也会变得非常昂贵。
如何知道需要多少样本才能达到统计上足够的分布?对这个问题的答案取决于你希望你的比较有多精确。样本之间的方差越低,你需要的样本数量就越少。标准差是一个告诉你分布中测量值的一致性的度量。可以通过动态限制基于标准差的基准迭代次数来实现自适应策略,也就是说,收集样本直到获得处于某个范围内的标准差。这种方法要求测量次数大于一次。否则,算法将在第一次运行基准测试之后停止,因为基准测试的单次运行具有 std.dev. 等于零。一旦标准差低于阈值,就可以停止收集测量。关于这种策略的更多细节可以在[@Akinshin2019, 第4章]中找到。
另一个需要注意的重要事项是是否存在异常值。使用置信区间将一些样本(例如,冷启动)丢弃为异常值是可以接受的,但不要故意从测量集中丢弃不需要的样本。对于某些类型的基准测试,异常值可能是最重要的指标之一。例如,在对具有实时约束的软件进行基准测试时,99百分位数可能非常有趣。Gil Tene在YouTube上有一系列关于测量延迟的讲座,涵盖了这个话题。
1. SPEC CPU 2017 benchmarks - http://spec.org/cpu2017/Docs/overview.html#benchmarks ↩
3. 另一种检查方法是运行正态性检验: https://en.wikipedia.org/wiki/Normality_test. ↩
6. Null hypothesis - https://en.wikipedia.org/wiki/Null_hypothesis. ↩
8. Mann-Whitney U test - https://en.wikipedia.org/wiki/Mann-Whitney_U_test. ↩
9. Kruskal-Wallis analysis of variance - https://en.wikipedia.org/wiki/Kruskal-Wallis_one-way_analysis_of_variance. ↩
12. 《计算机系统性能评估的工作量建模》一书 - https://www.cs.huji.ac.il/~feit/wlmod/. ↩